In order to use multi-formatted text, Database fields, scripts, Parameters, Calculated Fields within a single Field, Paragraph field can be a useful option.

To add a Paragraph field in FlexReportDesigner application:

1. Create a new FlexReport in C1FlexReportDesigner.
2. Bind it with Products Table.
3. From the Insert tab, add Paragraph field  to the report.
4. Double-click the Paragraph field to enter in edit mode.
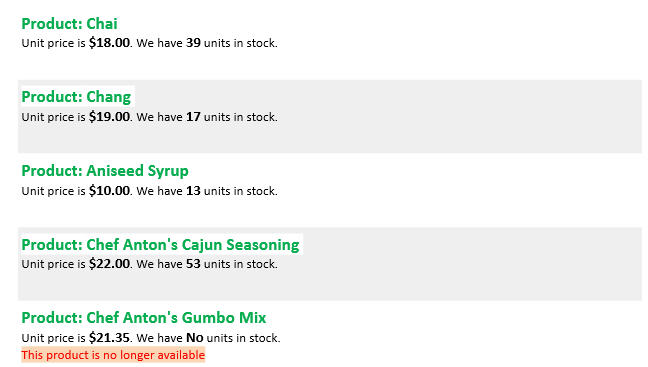
5. Type "Product:"

To insert Database fields:

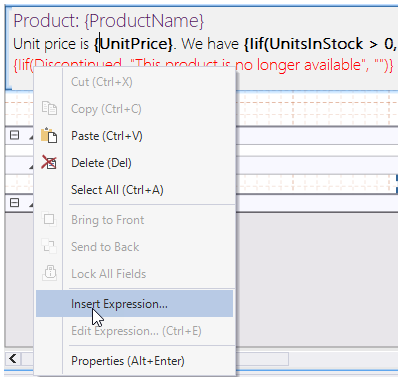
1. In edit mode, right-click the Paragraph field and select Insert Expression.
   
2. In the Expression editor, select 'ProductID' from DatabaseFields dropdown.
3. Click Done.
4. Select "Product:{ProductID}" and set ForeColor as Green from the Ribbon.

To change new line in edit mode:

1. In edit mode, press Ctrl+Enter.
2. In the next line, type static text "Unit Price is" and insert 'UnitPrice' Database Field using steps above.
3. Set {UnitPrice} as Bold.

To insert scripts:

1. After the text - "UnitPrice is {UnitPrice}", type - "We have".
2. Right-click and select Insert Expression.
3. Add following script: Iif(UnitsInStock > 0, UnitsInStock, "No")
4. Click Done.
5. After this script expression, type static text - "units in stock."
6. Select the script while in edit mode and set it to Bold.
7. Press Ctrl+Enter.
8. In newline, right-click and select Insert Expression.
9. Type following script: Iif(Discontinued, "This product is no longer available", "") /
10. Click Done.
11. Select the above mentioned script and set Highlight color to 'Orange, Accent 6 Lighter 60%' and ForeColor to Red.
12. Preview the report.