Part 2: Creating Custom Commands

In This Topic

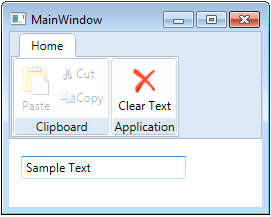
If the commands in the command library classes do not meet your needs, then you can create your own commands. You create a custom command by implementing the ICommand Interface. WPF provides a specific implementation named RoutedCommand (and RoutedUICommand), which defines a command routed through the element tree.

The following steps show how to add a custom command to C1Toolbar using a RoutedCommand.

Using the same sample from Part 1, open the code-behind file.
Define a RoutedCommand named ClearCommand. This command will be used to clear the text from the TextBox on the page.
```
public static RoutedCommand ClearCommand = new RoutedCommand();
```

Create an event handler which defines the command logic.

C#	Copy Code
// performs logic for ClearCommand private void ExecutedClearCommand(object sender, ExecutedRoutedEventArgs e) { textBox1.Clear(); }

Create another event handler which determines whether or not the command can be executed. When a command cannot be executed, the Toolbar buttons associated with the command will become grayed out and disabled.

C#	Copy Code
// only returns true if the textbox has text. private void CanExecuteClearCommand(object sender, CanExecuteRoutedEventArgs e) { if (textBox1.Text.Length > 0) { e.CanExecute = true; } else { e.CanExecute = false; } }

Copy Code

// only returns true if the textbox has text.
private void CanExecuteClearCommand(object sender, CanExecuteRoutedEventArgs e)
{
    if (textBox1.Text.Length > 0)
    {
        e.CanExecute = true;
    }
    else
    {
        e.CanExecute = false;
    }
}

Next, create a CommandBinding which associates the command with the event handlers. When the command is invoked, the element tree will be traversed looking for an object with a CommandBinding. Put this code after the InitializeComponent call for your page:

C#	Copy Code
CommandBinding customCommandBinding = new CommandBinding(ClearCommand, ExecutedClearCommand, CanExecuteClearCommand); // attach CommandBinding to root element this.CommandBindings.Add(customCommandBinding);

Copy Code

CommandBinding customCommandBinding = new CommandBinding(ClearCommand, ExecutedClearCommand, CanExecuteClearCommand);

// attach CommandBinding to root element
this.CommandBindings.Add(customCommandBinding);

In your XAML containing C1Toolbar, add a new C1ToolbarButton inside a group named Application.

Set the Command property to the static command in the code behind for your page.

XAML	Copy Code
<c1:C1ToolbarGroup Header="Application"> <c1:C1ToolbarButton LabelTitle="Clear Text" Command="{x:Static local:MainWindow.ClearCommand}" LargeImageSource="/Resources/clear.png"/> </c1:C1ToolbarGroup>

Run the application, and observe when the toolbar button is clicked, the ClearCommand is routed through the element tree looking for an associated CommandBinding. When found, the associated event handlers are called and your command logic performs.